Tarea 19 Teoría de conjuntos

Teoría de conjuntos

Existen unas operaciones básicas que permiten manipular los conjuntos y sus elementos, similares a las operaciones aritméticas, constituyendo el álgebra de conjuntos:

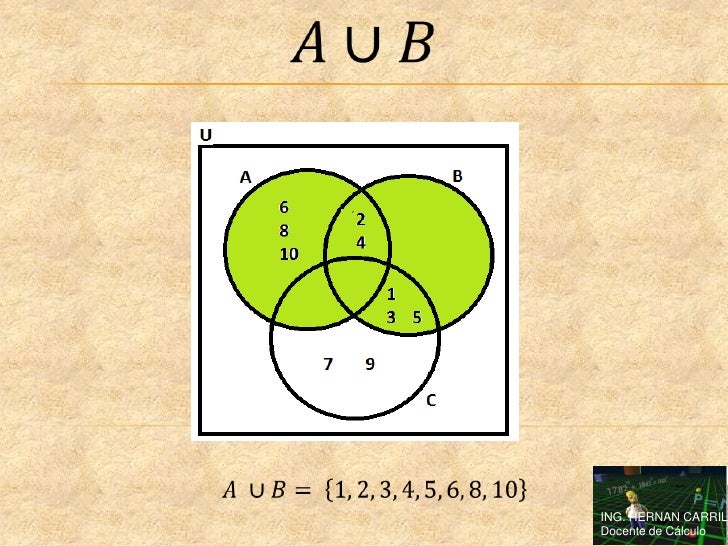
• Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene cada elemento que está por lo menos en uno de ellos.
• Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.
• Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.
• Complemento. El complemento de un conjunto A es el conjunto A^∁ que contiene todos los elementos (respecto de algún conjunto referencial ) que no pertenecen a A.

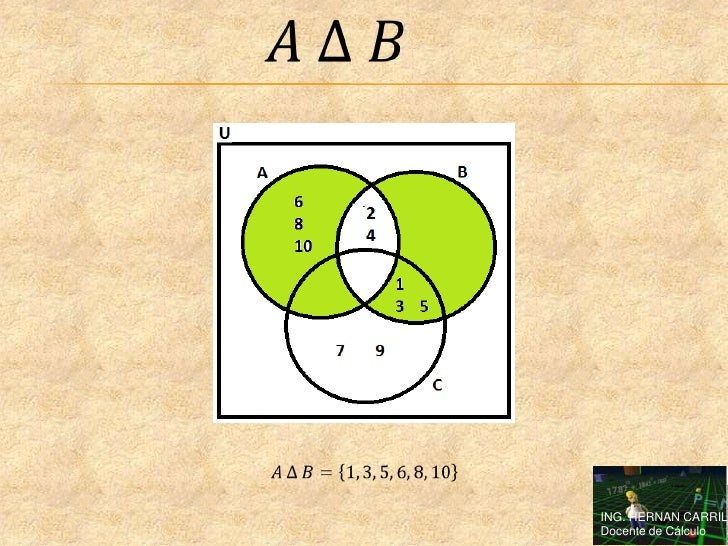
• Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
• Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento a pertenece a A y su segundo elemento b pertenece a B.

Una vez que se ha establecido un conjunto universal U de elementos de una cierta clase, se asume que todos los conjuntos Acontienen elementos de esta clase, por lo que todos ellos son subconjuntos de U. Esto conlleva una serie de propiedades:

Todo conjunto A es subconjunto de U, A⊆ U. La unión de un conjunto A con el conjunto universal U es igual a U: ${\displaystyle A\cup U=U}$ La intersección de un conjunto A con el conjunto universal resulta en el mismo conjunto A: ${\displaystyle A\cap U=A}$